Роботу виконав:
Кривошеєв Павло
учень 9 класу
Опитненського закладу загальної
середньої освіти І-ІІІ ступенів
Бахмутської міської ради
Донецької області
Науковий керівник:
Шумай Людмила Петрівна,
учитель хімії
Опитненського закладу загальної
середньої освіти І-ІІІ ступенів
Бахмутської міської ради
Донецької області
лауреатка V Всеукраїнського Інтернет-конкурсу
„УЧИТЕЛЬ РОКУ – 2020”
за версією науково-популярного
природничого журналу „КОЛОСОК”
у номінації „Хімія”
ВСТУП
Актуальність
У природі часто зустрічаються тверді тіла, що мають форму правильних багатогранників. Такі тіла назвали кристалами. Знаменитий вислів академіка О. Ферсмана «Майже весь світ кристалічний. У світі панує кристал і його тверді прямолінійні закони» повністю узгоджується з незгасним науковим інтересом вчених усього світу до кристалів. Завдяки новітнім відкриттям в галузі будови кристалічних тіл стався величезний стрибок у розвитку науки і техніки, сучасних засобів зв’язку, комп’ютерної техніки, космічних апаратів. Найголовніше – штучно вирощуючи кристали, створюють речовини, яких взагалі немає в природі. Тому опанування способами вирощування кристалів, вивчення їх властивостей є актуальним.
Мета дослідження: з’ясувати експериментальним шляхом способи вирощування кристалів в лабораторних умовах і спостерігати за процесом їх росту, довести анізотропію росту кристалів
Завдання: виростити кристали різних речовин, вивчити умови утворення кристалів, їх форму, дослідити анізотропію: залежність фізичних властивостей кристалів від обраного напрямку.
Об’єктом дослідження є кристали мідного купоросу, алюмокалієвих галунів, кам’яної солі, залізного купоросу, вирощені в умовах шкільної хімічної лабораторії.
Предмет дослідження: процес кристалізації, залежність фізичних властивостей від напрямку.
Методи дослідження: лабораторно-експериментальні, аналітичний, порівняльний.
Практичне значення. Матеріали наших досліджень можна використовувати на уроках фізики, хімії, географії, геометрії, факультативних та гурткових заняттях. Дослідження кристалів може бути частиною більшості шкільних дисциплін.
Структура та об’єм роботи. Робота містить 25 сторінок, малюнки, фотоматеріали
РОЗДІЛ І. ВНУТРІШНІЙ СВІТ КРИСТАЛІВ
У давні часи вважалося, що кристали являють собою рідкість. Дійсно, знаходження в природі великих однорідних кристалів – явище нечасте. Однак дрібнокристалічні речовини зустрічаються досить часто. Так, наприклад, майже всі гірські породи: граніт, пісковики, вапняк – кристалічні. У міру вдосконалення методів дослідження кристалічності виявилися речовини, до цього вважалися аморфними. Зараз ми знаємо, що навіть деякі частини організму кристалічні, наприклад, рогівка ока. В даний час вивченням різноманіття кристалів займається наука кристалографія. Вона виявляє ознаки єдності в цьому різноманітті, досліджує властивості і будова, як одиночних кристалів, так і кристалічних агрегатів. Завдяки цій науці відомі багато способів штучного вирощування кристалів. Деякі кристали навіть можна виростити в домашніх умовах. У природі можна зустріти такі кристали як гірський кришталь, флюорит, ісландський шпат, кам’яна сіль. На жаль їх не можна виростити без спеціальних приладів, але на щастя є безліч інших красивих кристалів, які можна виростити в домашніх умовах або навіть прикрасити ними будинок.
1. 1 Монокристали і полікристалічні тіла
Кристал (від грецького слова – krystallos, що означає лід) – тверді тіла, що володіють періодичною структурою і мають правильну геометричну форму.
Тіло, що представляє собою один кристал, називається монокристалом. Маленька крихта цукрового піску є монокристалом.
Більшість кристалічних тіл складається з безлічі хаотично розташованих і зрощених між собою дрібних кристаликів. Такі тіла називаються полікристалічний. Полікристалічними є все метали і мінерали. Шматок цукру теж полікристалічне тіло.
1. 2 Ідеальна форма кристалів
Правильна багатогранна форма кристала, перш за все, впадає в очі спостерігача, і вона, звичайно ж, не складає головну особливість кристалічного тіла, але все-таки я пропоную звернути увагу на це явище – ідеальну форму кристала.
Форму, яку приймає монокристал тоді, коли при його зростанні усунуті всі випадкові фактори, називають ідеальною. Ідеальна форма кристала має вигляд багатогранника. Такий кристал обмежений плоскими гранями, прямими ребрами і володіє симетрією. Як і всякий багатогранник, кристал має деяке число граней P, ребер R, вершин E, причому ці числа пов’язані між собою співвідношенням P + E = R + 2. наприклад, у куба 6 граней, 8 вершин і 12 ребер (6 + 8 = 12 + 2). Для октаедра (мал.1), додекаедра (мал.2) це співвідношення також справедливо.
Мал. 1–3.
Куб, октаедр, додекаедр є простими правильні багатогранники. У формі правильних багатогранників кристалізується порівняно невелике число кристалів. У формі куба кристалізується кухонна сіль, сірчистий цинк, в формі октаедрів – алмаз, у формі ромбічного додекаедра – гранат.
Найчастіше речовини кристалізуються у вигляді складних багатогранників, тобто вони бувають обмежені декількома сортами рівних між собою граней. Так, наприклад, кристал квасцов (рис.3) має зазвичай 6 восьмикутних граней, 8 шестикутних граней і 12 чотирикутних граней.
1.3 Закон сталості кутіва – основний закон кристалографії
Кристали одного і того ж речовини можуть мати вельми різноманітну форму. Форма кристала, як зазначалося вище, залежить від умов кристалізації. Колір також не є характерною ознакою кристалів даної речовини, так як він дуже сильно залежить від домішок. Відомо, наприклад, що кристали плавикового шпату можуть бути безбарвними, рожевими, чорними, фіолетовими, темно-вишневими і золотистими. Здавалося б, що встановлення належності двох кристалів (що відрізняються один від одного і формою і кольором) до однієї речовини не можна зробити інакше, як визначивши їх хімічний склад. Однак кристалографи встановили на перший погляд надзвичайно вражаючий факт: в кристалах однієї речовини кути між відповідними гранями завжди однакові (закон сталості кутів).
Що розуміють під відповідними гранями? В геометрії межі (плоскі багатокутники) вважаються рівними, якщо вони при накладанні співпадають усіма своїми точками. В кристалографії рівність граней означає зовсім інше. Грані можуть відрізнятися між собою за формою і все-таки вважатися рівними, якщо вони мають однакові фізичні і хімічні властивості. Встановити рівність граней в кристалографічному сенсі вдається іноді шляхом зовнішнього їх огляду.
Мал. 1–2.
У сумнівних випадках проводять травлення поверхні кристала кислотою. На рівних гранях малюнок, отриманий при травленні, буває однаковим.
На малюнку 1 однаковою штрихуванням показані однакові (рівні) грані. У кристалі кварцу можна встановити три сорти граней (на мал.2 вони відзначені буквами a, b і c). Хоча в різних кристалах кварцу межі a (b, c) мають різний розмір і форму, вони вважаються рівними. (В сучасних шкільних підручниках геометрії такі фігури називають конгруентними.)
Закон сталості кутів стверджує, що двогранний кут, утворений гранями a і b (мал.2) в різних кристалах даної речовини, буде один і той же. Відповідно у всіх кристалах даної речовини будуть рівні між собою і двогранні кути, утворені гранями a і c, b і c.
Отже, не форма кристалів, не розмір граней, а кут між ними є певною величиною для кожного кристала.
Мал. 3–4.
Для вимірювання кутів між гранями застосовують спеціальний прилад – гоніометр. Прикладний гоніометр (мал. 3) може бути застосований для дослідження великих монокристалів. Більш точні вимірювання виконують відбивних гоніометром, схема якого дана на малюнку 4. Пучок світла, що йде від джерела А, потрапляє на грань кристала і після відображення входить в підзорну трубу Т. При повороті кристала на певний кут пучок світла знову потрапляє в зорову трубу. За шкалою III гониометра відраховують кут між гранями. Вимірявши кути між гранями невідомого кристала, можна за спеціальним каталогом визначити хімічний склад кристала.
1.4 Про симетрію
З явищем симетрії ми часто зустрічаємося в нашому житті. Симетричний метелик (рис.1). Форма, малюнок і забарвлення лівого крила повторює форму, малюнок і забарвлення правого. Права рука людини симетрична лівої, бо при накладенні контури їх збігаються. Симетричні ваги з важелями. Будь-який предмет симетричний свого зображення в дзеркалі.
Мал. 1–2.
Якщо тіло можна подумки перетнути площиною так, що кожній точці a тіла з одного боку площини буде відповідати точка b, що лежить по іншу сторону площині і при тому так, що пряма ab, що з’єднує ці дві точки, перпендикулярна площині і ділиться цією площиною навпіл, то це тіло має дзеркальну симетрію. Сама площина називається в цьому випадку площиною симетрії. Наприклад, площина, проведена через середину ребер куба паралельно його обидва боки, служить площиною симетрії куба (рис.2). Куб має дев’ять площин симетрії.
Крім дзеркальної симетрії, тіла можуть володіти ще поворотною симетрією. Тіло має поворотну симетрію, якщо при повороті на відповідний кут всі частини фігури поєднуються одна з одною. Ось, навколо якої відбувається обертання тіла, називають віссю симетрії. Це залежить від того, скільки разів суміститься фігура сама з собою при одному повному повороті навколо осі, вісь симетрії має різний порядок (перший, другий, третій і т. п.).
Квітка ірису, наприклад, володіє віссю симетрії третього порядку (рис.3), сніжинки – віссю симетрії шостого порядку. В квітках дуже часто спостерігається вісь симетрії п’ятого порядку (мал.4).
Мал. 3–4.
Тіла можуть мати ще центр симетрії. Центр симетрії – точка в середині тіла, щодо якої будь-яка точка тіла має іншу відповідну їй точку, що лежить на такій же відстані від центру в протилежному напрямку.
У тілах може бути кілька площин симетрії, кілька осей симетрії різного порядку, але не може бути більше одного центру симетрії.
Якщо в параллелограмме, відігнути кути в протилежні сторони, то центр квадрата, отриманого в середині цієї фігури, буде центром симетрії, так як він ділить навпіл все прямі, попарно з’єднують однакові точки фігури. Геометричний центр кулі, куба, октаедра є центром симетрії цих тіл.
Вісь симетрії, площина симетрії і центр симетрії називають елементами симетрії. Елементи симетрії мають ряд властивостей. Ось деякі з них:
- Перетин двох площин симетрії дає вісь симетрії.
- Перетин трьох взаємно перпендикулярних площин симетрії дає центр симетрії.
1.5 Симетрія кристалів
Ідеальні форми кристалів симетричні. За висловом відомого російського кристалографа Євграфа Степановича Федорова (1853-1919), кристали блищать симетрією.
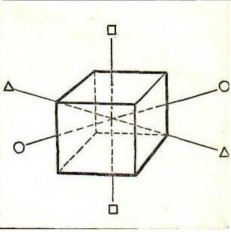
Мал. 1.
У кристалах можна знайти різні елементи симетрії: площина симетрії, вісь симетрії, центр симетрії.
Розглянемо симетрію деяких найпростіших кристалічних форм. Кристали в формі куба (NaCl, KCl та ін.) Мають дев’ять площин симетрії, три з яких проходять паралельно граням куба, а шість – по діагоналях. Крім того, куб має три осі симетрії 4-го порядку, чотири осі 3-го порядку і шість осей 2-го порядку (рис.1), крім того, він має центр симетрії. Всього в кубі 1 + 9 + 3 + 4 + 6 = 23 елемента симетрії.
Кристали алмаза, калієвих квасцов мають форму октаедрів. Октаедри володіють такими ж елементами симетрії, що і куби. На малюнку 2 показані осі обертання октаедра.
У кристалів магнію, що мають форму гексагональної призми (тобто призми, що спирається на правильний шестикутник), 6 площин симетрії і одна вісь симетрії 6-го порядку (мал.3). У кристалів мідного купоросу (мал4.). Є лише центр симетрії, інших елементів симетрії у них немає.
Мал. 2–4.
З цього невеликого огляду симетрій різних кристалів можна зробити висновок, що різні кристали володіють різною симетрією. Є форми багаті симетрією (куб, октаедр), є бідні (кристали мідного купоросу). У різних кристалів різні елементи симетрії. Наприклад, кристали магнію мають віссю симетрії 6-го порядку, а кристали NaCl мають 13 осей симетрії, але жодна з них не є віссю симетрії 6-го порядку і т.д.
Сукупність наявних елементів симетрії визначає вид симетрії. Так, можна стверджувати, що кристали кухонної солі (у вигляді кубів) і кристали калієвих квасцов (у вигляді октаедрів) мають однакову симетрією і відносяться до одного виду симетрії.
Кристали магнію, мідного купоросу мають свої своєрідні види симетрії.
На перший погляд здається, що число видів симетрії може бути нескінченно великим. Геометричні фігури (багатогранники) дійсно мають безліч видів симетрії. Однак серед кристалів невідомі осі обертання 5-го порядку, а також осі обертання вище 6-го порядку. Це обмежує число можливих видів симетрії кристалів. У 1867 р вперше з усією очевидністю російський інженер і кристаллограф А.В.Гадолін довів, що кристали можуть мати лише 32 класами симетрії.
1.6 Просторова решітка
Симетрія, закон сталості кутів і ряд інших властивостей! Як пояснити таку вередливість кристалічних форм?
Першою спробою наукового пояснення форми кристалів вважається твір Йоганна Кеплера “Про шестикутні сніжинки” (1611р.). Кеплер висловив припущення, що форма сніжинок (кристалів льоду) є наслідком особливих розташувань складових їх частинок.
У 1783 році французький абат Р. Ж. Гаюї, мінералог за покликанням, висловив припущення, що всякий кристал складений з паралельно розташованих рівних часток, суміжних з цілим гранях. У 1824 році учень великого Гаусса, професор фізики у Фрайбурзі Л. А. Зеебер для пояснення розширення кристалів при нагріванні запропонував замінити багатогранники Гаюї їх центрами ваг. Причому ці центри тяжіння утворюють правильну систему точок, яка згодом була названа просторової гратами, а самі точки – вузлами просторової ґрати. Наприклад, кристал кухонної солі NaCl складається із сукупності великого числа іонів Na+ і Cl-, певним чином розташованих одна відносно одної. Якщо зобразити кожен з іонів точкою і з’єднати їх між собою, то можна отримати геометричний образ, який малює внутрішню структуру ідеального кристала кухонної солі, його просторову решітку (мал.1).
Просторові решітки різних кристалів різні. На малюнку 2 показана просторова решітка алмаза, а на малюнку 3 – графіту.
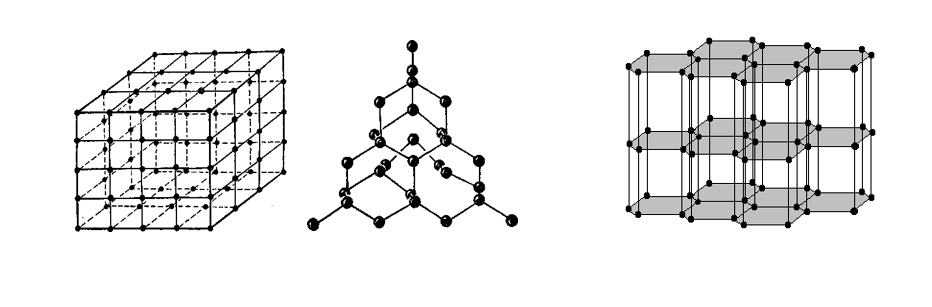
Мал. 1–3.
У кожній просторовій решітці можна виділити деякий повторюваний елемент її структури, або, інакше кажучи, елементарну комірку. Просторові, тобто об’ємні, а не плоскі елементарні осередки – це “цеглини”, прикладанням яких один до одного в просторі будується кристал. Так, елементарною клітинкою просторової ґрати NaCl є куб (рис. 4а). Дуже важливо тут відзначити, що існує багато способів побудови просторових решіток з елементарних осередків. “А скільки ж їх існує?” Ця складна задача була вирішена Е.С.Фёдоровим. Він довів, що повинно існувати 230 способів побудови кристала.
До найбільш простих елементарних осередків відносяться куб, об’ємно-центрований куб, гранецентрированний куб, гексагональна призма (мал. 4, а, б, в, г).
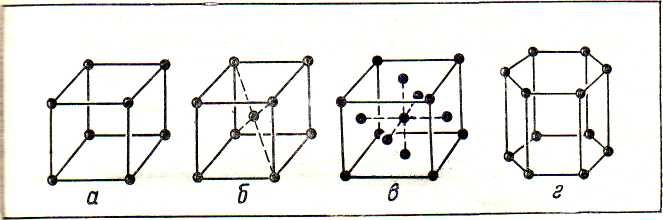
Мал. 4.
Гіпотеза про просторови решітки кристалів – свідоцтво про можливості наукового передбачення. Адже в той час (у другій половині XIX ст.) не тільки не існувало доказів цієї гіпотези, але і саме існування молекул і атомів речовини багатьма ставилося під сумнів.
Поняття про просторову решітку кристала виявилося дуже плідним, воно дозволило пояснити ряд властивостей кристалу.
Відомо, наприклад, що кристал, що має ідеальну форму, обмежений плоскими гранями і прямими ребрами.
Цей факт можна пояснити тим, що площина і ребра ідеального кристала завжди проходять через вузли просторової решітки.
Ставати також зрозумілим, чому кристали одного і того ж речовини можуть мати різноманітну форму. Подібно до того, як з даної плоскою сітки можна вирізати різні за формою площині фігури, так і кристал, маючи певну просторову гратку, може мати різну форму.
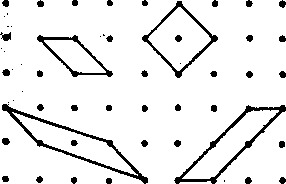
Мал. 5.
Просторова решітка дозволяє пояснити і основний закон кристалографії – закон постійності кутів. Якщо грань a (див. мал 2) пов’язана з однією площиною в кристалі, а грань b – з іншою, то, вочевидь, форма кристала (розмір окремих граней) не може позначитися на величині просторового кута між цими гранями. Останній визначається лише кутом між відповідними площинами в просторової решітці.
Однак плідність уявлення внутрішньої будови кристала у вигляді просторової решітки найбільш наочно проявляється в поясненні симетрії кристалів. Все розмаїття видів симетрії кристалів може бути доведено на основі симетрії просторових решіток. Симетрія кристалів є, таким чином, наслідком симетрії просторової ґрати.
Доказ цього факту мало велике значення для науки. Роботи Е. С. Федорова перетворили кристалографію в струнку теоретичну науку, піднявши її в кінці IX століття над усіма науками про будову твердих тіл.
1.7 Анізотропія кристалів
Істотною властивістю монокристалу є анізотропія – неоднаковість його властивостей (механічний, теплових, електричних та ін.) З різних напрямків. Наприклад, якщо кристали кухонної солі, що мають кубічну форму, розколювати, то дрібні осколки будуть мати переважно форму прямокутних паралелепіпедів. Це означає, що в напрямках, паралельних гранях, міцність кристала кухонної солі набагато менше, ніж в діагональних та інших напрямах.
Шматок слюди легко розшаровується в одному з напрямів на тонкі пластинки. Розшарувати його в напрямку, перпендикулярному пластинках, набагато важче. Також легко розшаровується в одному напрямку кристал графіту.
Якщо грань кристала, наприклад кварцу, покрити тонким шаром парафіну і доторкнутися до нього розпеченою голкою, то парафін почне плавитися. Розплавлений парафін має форми не кола, а еліпса, що вказує на відмінність теплопровідності кристала за різними напрямками. Про неоднаковості теплового розширення кристала за різними напрямками можна зробити висновок з наступного досвіду. Якщо з монокристала, наприклад кварцу, виготовити тіло кулястої форми і нагріти його, то після нагрівання воно вже не буде кулею. Уздовж трьох взаємно перпендикулярних діаметрів тіло розшириться неоднаково, а замість кулі вийде так званий еліпсоїд.
Полікристалічні тіла ізотропні, тобто виявляють однакові властивості у різних напрямах. Це пояснюється тим, що кристали, з яких складається кристалічне тіло, орієнтовані один відносно одного хаотично. В результаті жодне з напрямків не відрізняється від інших.
1.8 Процес утворення і росту кристалів
Швидкість росту кристалу за різними напрямками різна, так само різні і інші властивості кристала. Якщо обламати у кристала всі кути, сточити межі або виточити кульку і помістити його в холодний розчин або розплав того ж речовини, кристал буде рости. Якби він ріс в усі сторони однаково, то кулька, виростаючи, збільшувався б не змінюючи своєї форми. Він як і раніше був би кулькою. Але насправді це не так. В одних напрямках кристал росте, в інших він може розчинятися. Згодом збільшуючись, розширюючись, межі стикаються один з одним, і в кінці кінців весь куля стає многогранником; при цьому різні грані ростуть з різною швидкістю, тому і виникають різні форми кристалів. Таким чином, кристал, позбавлений своєї багатогранної форми, не втрачає здатності самоограняться. Багатогранна форма кристала залежить від того, що кристал росте нерівномірно, з різною швидкістю в різних напрямках.
Як же ростуть кристали в природі? У глибинах нашої планети знаходиться магма, тобто складний розчин-розплав з безліччю різних речовин, які утворюють при охолодженні різні мінерали з різною кристалічною будовою. Чому ж з однорідної магми виходять різні мінерали? Кожне хімічна речовина твердне або плавиться при певній температурі. Наприклад, якщо ви будете нагрівати кристал льоду, то до 0 ° кристал залишається незмінним. Але як тільки температура досягає 0 °, кристал раптом почне плавитися, причому, скільки б ми не гріли далі, температура льоду не підвищуватиметься, поки весь кристал, не розплавиться. Лише коли весь кристал перетвориться в воду, температура води почне підвищуватися. Якщо ж ми будемо охолоджувати воду, то точно при 0 ° рідину закрісталізуєтся, і її температура буде незмінною, поки вся вода не перетвориться на лід, після чого температура знову почне падати. Також і будь яка кристалічна речовина плавиться і кристалізується при строго певній температурі, характерною для неї, наприклад для кварцу 1713 °. У некристалічних тіл немає постійної температури плавлення (а отже, і температури кристалізації), при нагріванні вони розм’якшуються поступово. У склі вже і до нагрівання всі атоми розташовані безладно. При охолодженні розплавлене скло стає все більш в’язким і застигає поступово. Кристалічна ж речовина твердне відразу при певній температурі кристалізації. Коли в глибинах землі магма поступово застигає, хімічні речовини, що складають її, тверднуть не всі відразу а по черзі, тому що температура кристалізації їх різна. Тому магма розпадається на різнорідні, майже всієї складаються з кристалів мінерали.
РОЗДІЛ ІІ. МАТЕРІАЛИ ТА МЕТОДИКА ДОСЛІДЖЕННЯ
2.1 Матеріали та обладнання для вирощування кристалів
Найпростіша установка для вирощування кристалів з водних розчинів складається зі скляної банки 1, кришки 2, розчину 3 і вихідного кристала (зародка) 4)
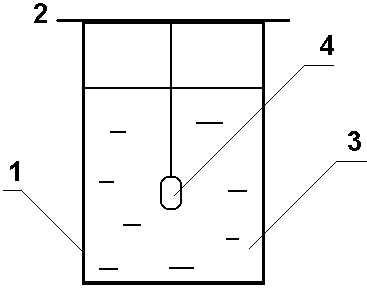Обладнання: сіль для вирощування кристалів, посудини на 500 мл, фільтрований папір або вата, товсті нитки, каркаси.
2.2 Вирощування кристалів з водних розчинів
Беремо сіль (наприклад, мідний купорос). Зважуємо грам 80. Робимо насичений розчин солі при високій температурі. Розчин ставимо остигати, кинувши туди пару-трійку кристалів солі (маленьких, які залишилися від розчинення). Після охолодження розчину витягаємо на фільтр осад надлишку солі, шукаємо там найбільші кристали, вибираємо їх, а інші розчиняємо в розчині 1 при кип’ятінні. Повторюємо ту ж операцію – кидаємо в гарячий розчин великі кристалики і ставимо охолоджуватися.
2.3 Вирощування кристалів з розчинів солей з використанням «затравки»
Спочатку приготуємо якомога більше концентрований розчин обраної солі, вносячи сіль в стакан з водою, до тих пір, поки чергова порція солі не перестане розчинятися при перемішуванні. Після цього злегка підогріємо суміш, щоб домогтися повного розчинення солі. Для цього склянку поставимо в каструлю з теплою водою. Отриманий концентрований розчин переллємо в банку або хімічну склянку; туди ж за допомогою дротяної перемички (можна також зробити перемичку з стрижня кулькової ручки) підвісимо на нитці кристалічну “затравки” – маленький кристалик тієї ж солі – так, щоб він був занурений в розчин. На цій “затравки” і належить рости майбутньому експонату нашої колекції кристалів. Через три доби після початку експерименту в першому склянці спостерігаємо нитку, опущену в насичений розчин, яка перетворилася в “намисто” з кристалів хлориду натрію, а в другому склянці на нитці з’явилися кристалики мідного купоросу. Судини з розчинами поставимо у відкритому вигляді в тепле місце. Коли кристали виростуть досить великими, виймемо їх з розчину, обсушити м’якою ганчіркою або паперовою серветкою, обрізаємо нитку і покриємо грані кристала безбарвним лаком, щоб оберегти від “вивітрювання” на повітрі.
Найважливіше умова: для вирощування кристалів використовують тільки свіже виготовлені розчини Так як в процесі стояння в розчинах у багатьох речовин накопичуються певного складу комплекси змінюють структуру кристала (такі кристали можуть починати швидше вивітрюватися). Якісь розчини сильно гідролізуються (їх ще можна очистити фільтруванням).
2.4 Приготування маточного розчину
Для приготування маточного розчину потрібно чистий, добре вимитий термостійкий стакан на 1 л. У нього наливають гарячу (t = 50о С, при високих температурах речовину сильно гідролізується) кип’ячену воду або, що краще, дистильовану 700-800 мл. У склянку засипають речовина невеликими порціями (1 порція = 1 столова ложка без гірки), кожен раз перемішуючи і домагаючись повного розчинення. Коли розчин «насититься», тобто речовина буде залишатися на дні, додають ще дві порції і залишають розчин при кімнатній температурі на добу. Щоб в розчин не потрапив пил, його накривають листом фільтрувального паперу і залишають в тій частині приміщення, де зберігається постійна температура, де в подальшому буде продовжений дослід. Якщо проходить опалювальний сезон, то можна залишити стакан і біля батареї, але пам’ятайте, що розчинність у речовини тепер буде інша. І якщо зміниться температурі, як виникне кристалізація – зайва речовина викристалізується з розчину. Щоб кристали росли як можна правильно, кристалізація повинна йти повільно, на безбарвних речовинах, яких кристали повинні бути прозорі як скло, швидкість зростання проявляється помітніше – при швидкому зростанні кристали каламутніють.
Можливий і зворотний спосіб приготування насиченого розчину. Максимально розчинити речовину при кімнатній температурі, і коли розчинення досягне межі (речовина буде залишатися на дні), додаєте ще 1-2 порції і нагріваємо посудину з розчином на плиті до t = 50-60о С. Умова цього способу – використовувана посуд повинна бути термостійкою, а конфорка плити рівною.
На наступний день оглядають розчин. Розчин мідного купоросу не повинен містити каламуті. На дні повинен випасти надлишок речовини у вигляді кристалів. У тому випадку, якщо виявлені домішки, розчин підігрівають на 20о C (поставте склянку з розчином в посудину з теплою водою на 1-2 години) і фільтрують на лійці, всередину якої поміщають фільтр або (що швидше і краще) шматочок вати. Оскільки нам осад не потрібен, навіщо ускладнювати процес фільтрування. Шматочок вати повинен лежати нещільно на дні воронки, щоб не заважати току рідини, але і не провалюватися з нею в стакан, інакше фільтрувати доведеться заново, змочувати вату водою, як фільтр не треба. Потім повторюють охолодження до кімнатної температури. Цей розчин буде необхідний нам у великій кількості, тому ви повинні мати посуд для його зберігання та в разі потреби запастися їм додатково. Зберігати його можна у колбі з притертою пробкою (якщо пробка гумова, то її обертають поліетиленовою плівкою, щоб вона не взаємодіяла з розчином), на дні повинні залишатися кристали речовини.
2.5 Отримання кристалу – затравки
Готовий очищений розчин акуратно зливають з осаду кристалів і в кількості 1 л поміщають в термостійку круглодонную колбу. Туди ж поміщають 1 чайну ложку (з гіркою) хімічно чистої речовини (це можуть бути ті ж випали кристали). Тепер колбу нагрівають на водяній бані, домагаючись повного розчинення, як правило, в забарвлених розчинах забарвлення, через надлишок речовини, стає інтенсивніше. Отриманий розчин гріють ще 5 хв на водяній бані при температурі не вище 60-70 оС, після чого його переливають в чистий, підігрітий до температури розчину термостійкий стакан (можна обполоснути окропом). Стакан обгортають щільно сухим рушником, накривають фільтрувальним папером і залишають остигати. Зараз розчин треба берегти від протягів, від різких перепадів температур. Різкий перепад температур, як і різке перемішування остиглого розчину, можуть викликати передчасну кристалізацію, але кристали при цьому вийдуть дрібні і безформні, вони щільно осядуть на стінки розчину і нагрівання доведеться повторювати знову.
Через добу, прибирають рушник, що не намагаючись колихати стакан, щоб не викликати незаплановану кристалізацію. Оглядають вміст – на дні і на стінках повинні утворитися невеликі плоскі сині кристали-паралелограми.
Якщо утворилося безліч дрібних зрощених безформних кристаликів, як після різкого охолодження, то кількість солі зменшують і повторюють описану стадію.
Якщо кристалики не утворилися, розчин не наситили як слід і тому розчину слід постояти ще добу; або слід збільшити кількість речовини, що розчиняється, повторивши етап заново.
Ця стадія експерименту навчає правильно вирощувати приманку, яка далі буде вихідною цеглинкою для отримання «величезною конструкції». Відберіть відповідні за структурою кристалики (з довгою ребра від 0,3 см і більше) і зберігайте їх окремо в банці з притертою пробкою далеко від джерел високих температур і світла. З якимось одним ви будете продовжувати експеримент. Чим менше обрана затравка, ніж вона правильніше, тим легше розчину (системі) підлаштуватися під неї.
РОЗДІЛ ІІІ. РЕЗУЛЬТАТИ ТА ЇХ ОБГОВОРЕННЯ
Вивчивши технологію вирощування кристалів, застосовували спосіб поступового охолодження насиченого розчину для вирощування кристалів мідного купоросу, залізного купоросу, алюмокалієвих галунів і кухонної солі.
Використовуючи цей спосіб, виконали наступні етапи:
- Виростили невеликі кристалики певної речовини
- Підготували насичений розчин цієї речовини на водяній бані.
- Гарячий розчин профільтрували
- В профільтрований розчин помістили кристалик, накрили серветкою и залишили на дві доби.
Експериментальним шляхом ми переконалися, що виростити монокристал дуже складно. Кристали виросли зрощеними: полікристали з яскраво вираженими плоскими гранями окремих кристалів та друза – це кристали, зрощені на загальній основі. Спостерігаючи за ростом кристалів помітили наступне: грані змінюють свої розміри-ростуть, але форма їх залишається незмінною, кути між відповідними гранями теж залишаються постійними. Упорядковане розташування частинок у монокристалі є причиною того, що монокристали мають плоскі грані та незмінні кути між гранями.
Якщо у кристала обламати всі кути, обточити грані, словом, позбавити його багатогранної форми, то його властивості не зміняться. Якщо кульку, вишліфувану з кристалу, помістити в її перенасичений розчин, вже через кілька годин на кулі з’являться крихітні рівні майданчики граней; поступово вони збільшаться, розширяться, і, врешті-решт, покриють всю кулю, перетворивши її в багатогранник. Чому ж все-таки кристали виростають багатогранними?
Тут проявляється одна із самих основних особливостей кристала – анізотропія його фізичних властивостей. Анізотропія – це неоднаковість фізичних властивостей речовин в різних напрямках (при цьому в симетричних напрямках властивості можуть виявитися однаковими). Анізотропія кристалів зумовлена їх кристалічними ґратками: в різних напрямках відстані між частинками, що утворюють кристалічну ґратку, різні (мал.).
Дослідним шляхом довели залежність механічної міцності, теплопровідності від напрямку. Для дослідів використовували природні кристали кам’яної солі, які були взяті з соляної шахти. Якщо вдарити молоточком по кристалу, він розбивається на кубики з рівними, гладкими, плоскими гранями Механічна міцність кристалів різна в різних напрямках.
Дослідження теплопровідності кристалів проводили так :наносили краплю парафіну на різні грані кристалів і давали їй застигнути. Потім доторкалися до цих граней добре прогрітою спицею і спостерігали за формою краплі парафіну. В одних випадках форма була кругла, а в інших витягнута, а це значить, що в першому випадку тепло поширювалося в усіх напрямках однаково, а в другому – тепло поширювалося в одних напрямах повільніше, а в інших – швидше і форма краплинки була вже не круглою. Різна в різних напрямках теплопровідність.
ВИСНОВКИ
Досліджуючи різні способи вирощування кристалів з водного розчину ми довели, що майже всі фізичні властивості кристалів анізотропні. Анізотропна і швидкість росту кристала. Якби швидкість росту кристалів не залежала від напрямку, була б у всіх напрямках однаковою, то кристал ріс би в усі сторони однаково і міг би мати тільки форму кулі, як крапля олії у воді. Саме тому, що зростає він у різні боки з різними швидкостями, і виросте він багатогранником. Кристали зустрічаються нам всюди. Ми ходимо по кристалам, будуємо з кристалів, обробляємо кристали на заводах, вирощуємо кристали в лабораторіях і в заводських установках, створюємо прилади та вироби з кристалів, широко застосовуємо кристали в техніці і в науці, їмо кристали, лікуємося ними, знаходимо кристали в живих організмах, проникаємо в таємниці будови кристалів. Майбутнє новітніх технологій належить кристалам і кристалічним агрегатам.
Література
1. Мала гірнича енциклопедія. В 3-х т. / За ред. В. С. Білецького. — Донецьк: «Донбас», 2004.
2. Веннинджер М., Модели многогранников / Пер. с англ. / М: «Мир», 1974. – 236 с.
3. Гегузін Я. Е., Живий кристал / М: «Наука», 1981
4. Кожухарів А. С. Утворення кристалів / М. — Л., 1947.
5. Лодіз Р. А., Паркер Р. Л.Зростання монокристалів / Пер. з англ. / М., 1973.
6. Маллін Дж. Кристалізація / Пер. з англ.. / М., 1966.
7. Шевченко Л.Л. Кристалохімія / К: «Вища школа», 1993. – 169 с.8.
9. http://shron1.chtyvo.org.ua/Fodchuk_Ihor/Osnovy_krystalohrafii.pdf
10. http://course-crystal.narod.ru/p35aa1.html
ДОДАТКИ
Алюмакалієві галуни
Редакція може не поділяти думку авторів і не несе відповідальність за достовірність інформації. Будь-який передрук матеріалів з сайту може здійснюватись лише при наявності активного гіперпосилання на e-kolosok.org, а також на сам матеріал!
